Pengertian Gerak Parabola, Rumus, Soal, dan Pembahasannya

Gurubagi.com. Jika kita membayangkan parabola televisi, sebenarnya terdapat kesamaan dengan gerak parabola. Lintasan gerak parabola melengkung mirip parabola televisi, akan tetapi tidak penuh.

Gerak parabola adalah gerak dimana lintasannya tidak bergerak lurus tapi membentuk parabola. Hal ini terjadi karena adanya perpaduan antara gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB).

Kedua gerak tersebut membentuk suatu sudut elevasi pada sumbu x (horizontal) dan sumbu y (vertikal), di mana sumbu x merupakan GLB dan sumbu y merupakan GLBB. Dengan begitu, keduanya membentuk lintasan melengkung yang disebut gerak parabola.

Rumus Gerak Parabola

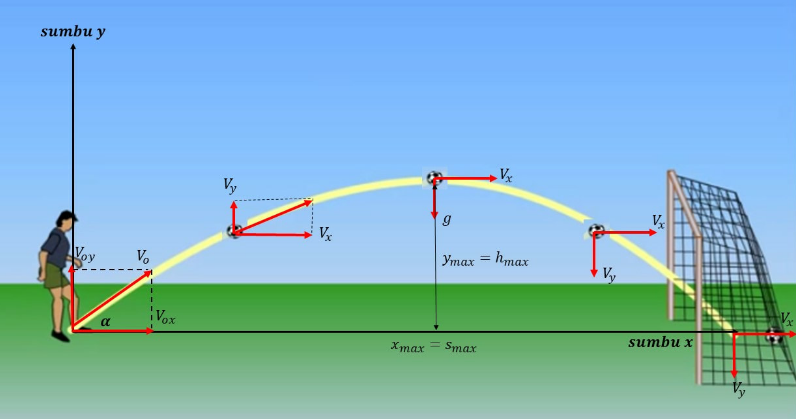
Rumus gerak parabola terbagi ke dalam dua sumbu yaitu sumbu x dan sumbu y. Komponen pada gerak ini yaitu titik O yang merupakan titik awal benda.

Rumus gerak parabola diuraikan dalam 2 sumbu, sebagai berikut.

1. Rumus gerak parabola pada sumbu x

Vx = V₀x = V₀.Cosα

Jika jarak dalam arah sumbu x, maka diperoleh rumus berikut.

x = Vx .t

dimana :

v_x = kecepatan akhir benda pada sumbu x (m/s) ;
v₀ = kecepatan awal benda (m/s)
α = sudut elevasi yang terbentu antara sumbu x dengan lintasan
t = waktu yang dibutuhkan untuk menempuh lintasan parabola

sedangkan untuk penuisan sistematis yang diuraikan pada sumbu y sebagai berikut :

v_y = v_oy – gt

bila ditinjau pada sumbu vertika v_0y= v₀ sin α, maka

V_y = v_osinα – gt

2. Rumus gerak parabola pada sumbu y

Jika kecepatan berupa fungsi waktu (berubah tergantung waktu)

Vy = V₀ sin α – gt

Jarak dalam arah sumbu Y dapat ditentukan dengan rumus berikut

y = V₀ sin α t – ½ gt²

dimana :

v_y = kecepatan akhir benda pada sumbu y (m/s) ;
v_0y = kecepatan awal benda (m/s)
α = sudut elevasi yang terbentu antara sumbu x dengan lintasan
t = waktu yang dibutuhkan untuk menempuh lintasan parabola

Beberapa persamaan khusus pada materi gerak parabola sebagai berikut.

a. Kecepatan benda dalam gerak parabola yang diuraikan pada komponene sumbu x dan sumbu y dapat dituliskan sebagai berikut :

v₀x = V₀.Cosα

v₀y = V₀.sinα

b. Arah benda gerak parabola pada komponen sumbu-x bisa dituliskan sebagai berikut.

tan θ = vy / vx,

sehingga nilai v_x selalu positif, tetapi juga bergantung pada nilai v_y.

c. Pada komponen sumbu y, benda akan memiliki kecepatan = 0 ketika benda pada posisi tinggi maksimum, sehingga penulisan sistematisnya sebagai berikut : tAB = (v₀ sinα)/ g

d. Tinggi maksimum benda pada komponen sumbu x, yaitu H =( v₀² sin²α)/2g

e. Jarak tempuh maksimum benda pada komponen sumbu-x, yaitu:

X = v₀xt_AC = v₀cosα 2(v0 sinα/g) = v₀²2 (sinα/g) cos α

X = ( v₀2 sin²α)/g

Baca :

Soal Gerak Parabola

Soal nomor 1

Joko menendang bola dengan sudut elevasi 45^o. Bola jatuh dengan jarak mendatar sejauh 5 m. Jika percepatan gravitasi bumi 10 m/s², hitunglah kecepatan awal bola!

Pembahasan:

Diketahui:

g = 10 m/s²

α = 45^o

Ditnyakan v_o?

Jawab:

Menghitung kecepatan awal jika jarak terjauh diketahui:

x = v_o² sin 2α x 1/g

5 = v_o² sin (2×45) x 1/10

5 = v_o² sin 90 x 1/10

= v_o² x 1 x 1/10

50 = v_o²

v_o = √50

v_o = 5√2 m/s

Soal nomor 2

Sebuah peluru ditembakkan dengan lintasan. Lintasan dapat dilihat pada gambar dibawah apabila gravitasi adalah 10 m/s². Hitung tinggi maksimum yang dicapai peluru!

Pembahasan:

Diketahui :

kecepatan awal diam (v_o) = 20 m/s

sudut elevasinya (α) = 30°

gravitasi (g)=10 m/s²

Ditanya : Tinggi maksimum?

Jawab:

Mencari ketinggian maksimum

H = vo²sin²α/2g

= 20².sin²30/ 2.10

= 400.(¹/₂)²/20

= 5 meter

Soal nomor 3

Apabila sebuah peluru ditembakkan dengan kecepatan tertentu yaitu 20 m/s. Jika peluru mencapai titik tertinggi setelah √3 sekon dan dan percepatan gravitasi = 10 m/s² tentukan sudut elevasinya!

Pembahasan:

Diketahui :

waktu saat dititik tertinggi ™ = √3 sekon

kecepatan awal (vo) = 20 m/s

gravitasi (g)=10 m/s²

Ditanya :

sudut elevasinya (α) = ?

Jawaban:

Mencari ketinggian maksimum

tm = √(2Hm)/(g)

√3 = √(2.Hm)/(10)

√3 = √(2Hm)/(10)

√3 = √(Hm/5)

Hm/5 = 3

Hm = 3.5 = 15 meter

Mencari Sudut elevasi

Hm = vo²sin²α/2g

15 = 20².sin²α/ 2.10

15 = 400.(sin α)²/20

300 = 400.(sin α)²

300/400 = (sin α)²

√(3/4) = sin α

¹/₂√3 = sin α

α = 60°

Jadi, sudut elevasinya (α) adalah 60°

Soal nomor 4

Apabila diketahui sebuah peluru ditembakkan dengan kecepatan 20 m/s jika sudut elevasinya 60° dan percepatan gravitasi = 10 m/s² maka peluru mencapai titik tertinggi setelah

Pembahasan:

Diketahui :

kecepatan awal diam (v_o) = 20 m/s

sudut elevasinya (α) = 60°

gravitasi (g)=10 m/s²

Ditanya :

waktu saat dititik tertinggi ™ ?

Jawab:

Mencari ketinggian maksimum (Hm)

Hm = vo²sin²α/2g

= 20².sin²60/ 2.10

= 400.(¹/₂√3)²/20

= 15 meter

waktu saat dititik tertinggi

tm = √(2Hm)/(g)

tm = √(2.15)/(10)

tm = √(30)/(10)

tm = √(3) = √3 sekon

Jadi, waktu saat dititik tertinggi adalah √3 sekon

Demikian pengertian gerak parabola, rumus, soal, dan pembahasannya. Semoga bermanfaat.

Pengertian Gerak Parabola, Rumus, Soal, dan Pembahasannya