Ketidakpastian dalam Pengukuran dan Contoh Soalnya
Gurubagi.com.Pengukuran merupakan dasar yang sangat penting. Dalam setiap pengukuran atau percobaan, ketidakpastian dan ketidaktelitian selalu ada.
Pengukuran adalah kegiatan membandingkan besaran yang akan diukur dengan besran sejenis yang telah ditetapkan sebagai satuan yang ditetapkan secara internasional.
Suatu hasil pengukuran selalu mengandung ketidakpastian atau kesalahan karena dalam setiap pengukuran memungkinkan terjadi gangguan, baik objek ukur ataupun alat ukurnya.
Maka hampir dapat dipastikan tidak ada hasil ukur yang nilainya tepat sama dengan nilai sebenarnya.Ketidakpastian dikelompokkan ke dalam 3 macam :
1. Kesalahan umum atau gross error
Kesalahan umum atau gros error merupakan kesalah yang terjadi oleh manusia atau orang yang mengukur itu sendiri antara lain :
a. Kesalahan pada saat membaca alat ukur
b. Penyetelan alat ukur yang tidak tepat
c. Kelemahan mata kita yang pada umumnya tidak bisa melihat secara baik skala atau benda yang lebih kecil dari 1 mm.
d. Pemakaian insrumen yang tidak sesuai
e. Kesalahan peaksiran dan paralaks (perbedaan hasil pengukuran karena kita melihat pada sudut yang berbeda.
f. Pengaruh meniskus pada tabung. meniskus terjadi jika kita mengukur air dalam gelas ukur.
2. Kesalahanyang tidak disengaja/ kesalahan acak random error
Kesalahan acak disebabkan oleh gejala yang tidak dapat secara langsung diketahui sehingga tidak mungkin dikendalikan secara pasti atau tidak dapat di atasi secara tuntas.
Kesalah ini dapat disebebkan oleh beberapa sebab diantaranya:
- Adanya pengaruh lingkungan berupa getaran yang dapat mempengaruhi hasil pengukuran.
- Adanya fluktuasi tegangan yang menyebabkan kesalahan dalam pengukuran
- Adanya radiasi gelombang elektronik yang menyebabkan terjadinya kesalahan pengukuran
3. Kesalahan Sistematis atau systematic errors
Kesalahan sistematis ini terjadi berasal dari alat ukur yang dgubakan atau kondisi pada saat melkaukanpengukuran. Berikut ini termasuk penyebab ketidakpastian sistemtik adalah karena :
a. Kesalahan kalibrasi alat
Seringkali terdapat beberapa alat ukur yang skalanya sembarangan dan tidak memenuhi ketentuan. Dalam beberapa hal, kesalahan ini sengaja untuk mencurangi pembeli, misalnya memberati timbangan, “mencurangi” meteran listrik, meteran POM bensin dan lain-lain.
Kesalah yang terjadi karena memberi nilai skala pada saat pembuatan alat tidak tepat sehingga berakibat terjadinya kesalahan pa setiap kali alat digunakan. Kesalah ini dapat di atasi dengan cara mengkalibrasi ulang alat terhadap alat standar.
Baca : Notasi Ilmiah : Pengertian dan Penjelasannya
b. Kesalah nol
Usia atau lama pemakaian sehingga menyebabkan bagian-bagian alat ukur aus atau kesalahan di titik nol pada alat ukur. Misalkan alat ukur yang sudah tidak bisa dikalibrasi lagi sehingga mengalami kesalahan titik nolnya
Ketidakpastian atau kesalahan ini dapat terjadi karena dalam setiap pengukuran memungkinkan terjadi gangguan, baik kepada objek ukur maupun pada alat ukur, baik kepada besaran yang diukur maupun kepada alat yang digunakan untuk mengukur.
Terdapat dua jenis ketidakpastian yaitu:
1. Ketidakpastian mutlak
- Ketidakpastian mutlak pengkuran tunggal
Pengukuran tunggal adalah pengukuran yang dilakukan hanya satu kali saja, apapun itu alasannya.
Hasil pembacaan skala yang dapat diketahui dengan pasti adalah hanya sampai kepada skala terkecilnya saja selebihnya adalah hanya terkaan atau taksiran. Pengukuran tunggal ini dirumuskan dengan :
X = Xo ± ΔX
Keterangan :
X = nilai besaran yang diukur
Xo =hasil pengukuran
ΔX = ketidakpastian atau kesalahan
Untuk menentukan Δ𝑥 dapat menggunakan rumus ketidakpastian pengukuran tunggal seperti di bawah ini:
Δ𝑥 = ½ nst
Nst atau nilai skala terkecil merupakan ukuran terkecil yang bisa dilaporkan dalam pengukuran.
Contoh
Dimas akan melakukan pengukuran tunggal dengan menggunakn alat ukur penggaris. Dimas ingin mengetahui berapa panjang pensil yang dia gunakan. Perhatikan gambar di bawah ini.

Pebahasan :
Jawab :
Pengukuran tunggal ini dirumuskan dengan :
X = Xo ± ΔX

Panjang pensil terletak di antara 6,4 cm dan 6,5 cm, sehingga nilainya akan bervariasi, bisa 6, 45 cm, 6, 46 cm, atau bahkan 6, 47.
Misalnya pada penggaris, berarti nst-nya yaitu jarak antara garis pertama dengan garis kedua. Dari gambar di atas tersebut, kita tahu kalau nst penggaris yaitu 6 mm = 0,6 cm.
Nilai Skala Terkecil (NST) mistar yang di gunakan adalah 0,1 cm, maka besar ketidakpastian mutlaknya adalah:
Maka nilai Δ𝑥 penggaris, yaitu:
Δ𝑥 = ½ nst
Δ𝑥 = ½ . 0,1 = 0,05 cm
Karena Δ𝑥 memiliki dua angka desimal, maka Xo juga harus memiliki dua angka desimal. Panjang pensil yang Dimas ukur sebelumnya berada di antara 6,4 cm dan 6,5 cm.
Dengan begitu kita harus mengubahnya menjadi dua angka desimal sehingga Xo = 6,46 cm.
Dengan demikian, hasil pengukurannya bisa ditulis 𝑥 = (6,46± 0,05) cm. Ini artinya, panjang penghapus terletak di antara 6,46 – 0,05 dan 6,4 + 0,05. Dapat juga ditulis seperti dibawah ini:
(6,46 – 0.05) < x < (6,46 + 0,05) atau 6,41 < x < 6,51
X = 6,36 ± 0,05
2. Ketidakpastian mutlak pengukuran berulang
Hasil pengukuran dan ketidakpastian pengukuran berulang ditentukan berdasarkan semua hasil ukur yang telah diperoleh. Hasil pengukuran beulang dapat dinyatakan dengan pola :
(x ± ΔX)
Dimana : x = hasil pengukuran nilai rata-rata (pengukuran berulang)
ΔX = ketidakpastian mutlak pengukuran
Ketidakpasatian pengukuran mutlak ditentukan dengan rumus simpangan baku (standar deviasi),yaitu :
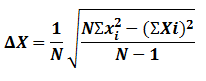
Dimana :
N = jumlah pengulangan pengukuran
Xi = hasil pengukuran ke-i
Ketidakpastian Relatif
Ketidakpastian relatf merubandingan ketidakpakan persentase perbandigan ketidakpastian mutlak dengan hasil pengukuran terbaik
- Ketidalpastian relatif relatif untuk pengukuran tunggal ditentuka dengan :
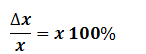
- Ketidakpastian relatif untuk pengukuran berulang ditentukan dengan :
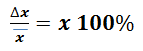
Semaki kecil ketidakpastian relatif, maka makin tepat pengukuran tersebut. Nilai ketidakpastian dalam pengukuran akan mempengaruhi jumllah angka berarti yang boleh diikutsertakan alam penulisan.
Semakin besar jumlah angka berarti yang boleh diikitsetakan maka semakin tepat pengukuran tersebut. Adapun ketentuan jumlah angka berart (angka penting) yang boleh dilaporkan adalah :
- Ketidakpastian relatif 10% berhak atas dua angka berarti
- Ketidakpastian relatif 10 berhak atas tiga angka berarti
- Ketidakpastian relatif 0,1,% berhak atas empat angka berarti
Contoh Soal
Jika Dimas melakukan pengukuran terhadap pensil sebanyak 6 kali didapatkan data yaitu : 12,0 cm, 11,9 cm, 12,22 cm, 11,8 cm, 12,1 cm, dan 12 ,4 cm. Tentukan laporan ketidakpastianya
Pembahsan :
Untuk mempermudah dalam perhitungan perhatkan tabel di bawah ini
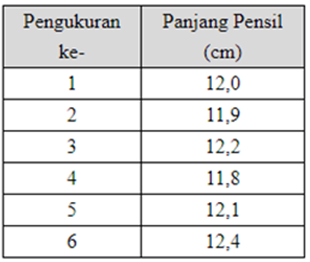
Jawab :
Rumus
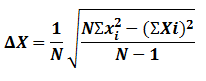
Untuk mempermudah perhatikan data di bawah ini!
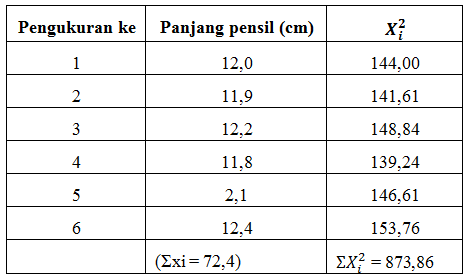

Karena ketidakpastian relatif dekat dengan 1%, maka pelaporan hasil pengukuran hanya berhak dengan 3 angka, Jadi penulisan hasil pengukuran adalah x = 12.1 ± 0,08 cm.
Demikian ketidakpastian dalam pengukuran dan cntoh soalnya. Semoga bermanfaat

