Besaran Vektor : Pengertian dan Cara Menentukan Gambarnya
Gurubagi.com. Besaran vektor termasuk materi fisika yang dibahas dalam Bab 1 Kelas XI SMA pada Kurikulum Merdeka.
Besaran dalam fisika dapat dikelompokkan berdasarkan ada tidaknya arah, dalam hal ini besaran jenis ini terdapat dua, yaitu besaran skalar dan besaran vektor.
Di dalam artikel ini kita akan membahas tentang besaran vektor berkenaan tentang pengertian, lambang, notasi vektorcara dan menentukan gambarnya .
Besaran vektor adalah besaran yang mempunyai nilai (besar) dan arah. Contoh besaran vektor, antara lain, perpindahan, kecepatan, percepatan, momentum, gaya, momen gaya, medan listrik dan medan magnet.
Contoh besran vektor dalam kehidupan sehari-hari kalian dapat perhatikan gambar di bawah. Pada saat sesorang duduk di atas kursi maka orang tersebut akan memberikan tekanan ke arah bawah pada kursi.

Simbol vektor
Simbol besaran vektor dapat dinyatakan degan hurup cetak tebal atau hurup cetak tipis yang diberi tanda panah di atasnya. berikut ini simbul untuk penulisan vektor.
a. Dalam satu hurup
vektor yang digambarkan dalam satu hurup dapat berupa hurup besar atau hurup kecil.
Contoh :
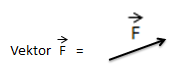
d. Dalam dua huruf
Contoh :
![]()
Titk A menunjukan titik asal vektor, titik B menujukan arah vektor (titik terminal) dan panjang garis menunjukan nilai atau bsarnya vektor
Menggambarkan vektor
Cara menggambarkan vektor adalah dengan menggambarkan sebuah anak panah dimana panjang anak panah sesuai dengan nilai vektor dan arah anak panah sesuai dengan arah vektornya. Vektor ditentukan arahnya dengan menggunakan sudut.
Sebuah vektor dilukiskan dengan sebuah anak panah dimana:
- Panjang panahnya disesuaikan dengan besar vektor tersebut.
- Arah anak panah mewakili arah vektor. Umumnya arah vektor menggunakan sumbu x positif sebagai titik acuannya.
Misalnya, Andi (A) berjalan dengan sudur 50o ke arah timur dengan jarak 100 m, maka anak panahnnya akan menjadi seperti di bawah ini;
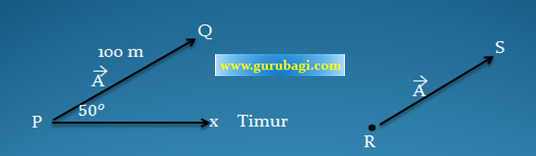
Untuk menetukan vektor, terlebih dahulu harus mengetahui arah di mana vektor tersebut, misalnya berjalan ke arah timur, sehingga dapat menetukan sudutnya, garis menuru sudut dan dapat menentukn arah vektor tersebut.
Resultan Vektor (R)
Beberapa vektor dapat dijumlahkan menjadi sebuah vektor yang disebut resultan vektor. Resultan vektor dapat diperoleh dengan beberapa metode, yaitu metode segitiga, metode jajargenjang, poligon, dan analitis. Berikut ini penjelasnnya
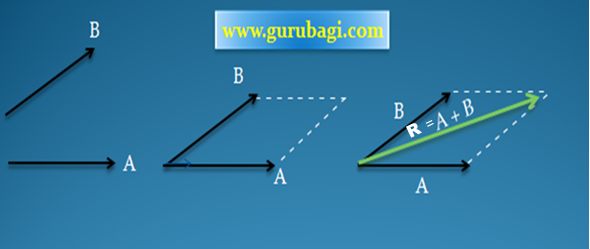
a. Metode jajar genjang
Untuk menentukan resultan dengan metode jajargenjang terdapat beberapa langkah, yaitu sebagai berikut.
- Lukis terlebih dahulu vektor pertama dan vektor kedua dengan titik pangkal berimpit.
- Lukis sebuah jajargenjang dengan kedua vektor tersebut sebagai sisi-sisinya.
- Resultan kedua vektor adalah diagonal jajargenjang yang titikpangkalnya sama dengan titik pangkal kedua vektor. .
- Pada metode jajargenjang, satu kali lukisan hanya dapat digunakan untuk mencari resultan dua buah vektor.
- Untuk resultan yang terdiri atas tiga buah vektor diperlukan dua jajargenjang, empat buah vektor diperlukan tiga jajargenjang, dan seterusnya.
Perhatikan gambar di bawah ini.
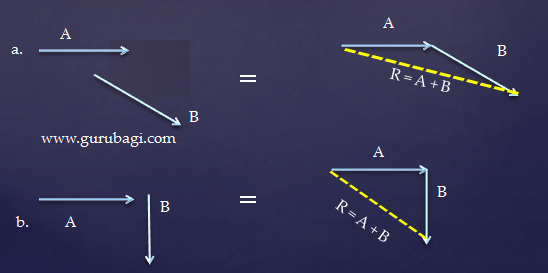
b. Metode segitiga
Dalam vektor kita juga harus tahu cara melukis penjumlahan atau selisih vektor tersebut. Vektor dijumlahakan memiliki metode melukis vektor yaitu metode segitiga dan metode jajar genjang untuk 2 vektor yang dijumlahkan.
Perhatikan gambar di bawah ini
 .
.
Dari gambar di atas, dapat di lihat sebernarnya resultan kedua vektor itu sama yang membedakannya hanya metode melukiskan vektor yang berbeda.
Baca : Pengertian Besaran Skalar, Contoh, dan Cirinya
Untuk vektor dengan metode segitiga, kita harus tahu arah keduanya vektor akan mengarah ke vektor, contoh di atas adalah A ke B (lihat panah arah A dan B). Akan tetapi, jika arah vektor berlawan tidak bisa kita gunakan metode segitiga.
c. Metode poligon
Untuk menentukkan resulatan vektor lebih dari 2 vektor, maka kita gunakan metode poligon untuk lebih jelas perhatikan gambar di bawah ini.
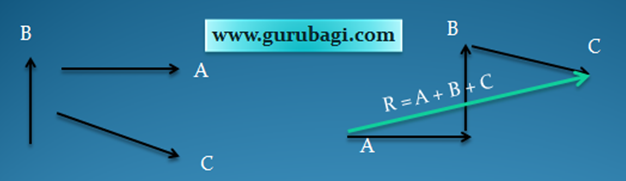
Dari gambar di atas dapat dsimpulkan bahwa, pada metode poligon sama dengan metode segitiga karena berdasarkan arah vektor berjalan.
Kita lihat pada metode poligon di atas Vektor A mengarah ke Vektor B, lalu Vektor B mengarah ke Vektor C, dan resultannya tinggal kita menarik garis dari vektor A ke Vektor C.
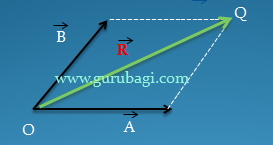
d. Metode Analisis
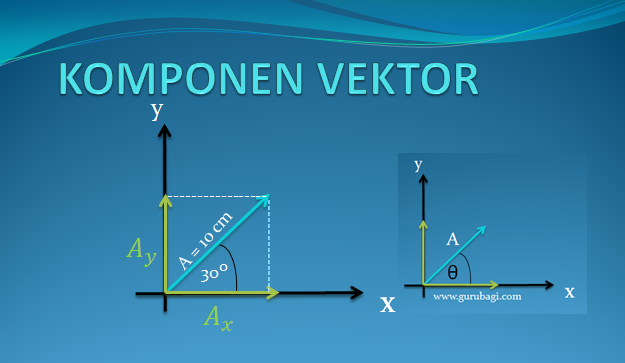
Metode yang paling tepat untuk menentukan resultan beberapa vektor dan arahnya adalah metode analisis. Metode analisis adalah cara menentukan resultan vektor melalui proses penguraian vektor menjadi vektor-vektor komponennya.
Vektor komponen adalah hasil proyeksi suatu vektor trhadap sumu X dan sumbu Y pada bidang cartesius yang saling tegak lurus.
Metode ini, mencari resultan dengan cara perhitungan bukan pengukuran, yaitu menggunakan rumus kosinus dan mencari arah vektor resultan dengan menggunakan rumus sinus seperti penjelasan di bawah ini..
a. Rumus kosinus.
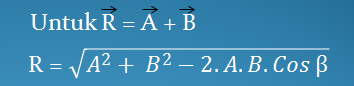
dan
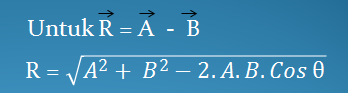
b . Rumus sinus (arah vektor)
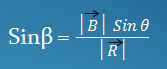
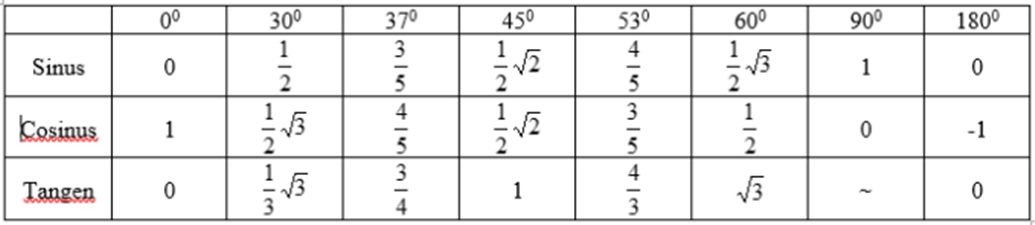
Berikut ini besar sudut-sudut istimewa yang biasa dugunakan da mungkin dibutuhkan sebagai acuan dalam meghitung resultan dengan menggunakan metode analisis
Demikian besaran vektor pengertian notasi dan cara menggambarnya. Semoga bermanfaat