Penjumlahan Vektor Metode Jajar Genjang Berikut Contoh Soalnya
Gurubagi.com. Penjumlahan vektor dapat dilakukan dengan beberapa metode, salah satunya adalah penjumlahan dengan metode jajar genjang.
Penjumlahan dengan metode jajar genjang adalah metode yang mengaitkan pangkal dengan pangkal. Penjumlahan vektor dengan metode jajar genjang dilakukan dengan merangkai setiap vektor sedemikian sehingga pangkal setiap vektor berhimpitan di satu titik.
Setelah itu dibuat proyeksi untuk setiap vektor dan proyeksi tersebut ditempatkan sedemikian sehingga membentuk jajar genjang dan di tarik garis diagonal sebagai resultan vektor.
Resultan vektor adalah diagonal jajar genjang dengan pangkalnya berhimpitan dengan vektor lain. Berikut ini cara menjumlah A dan B (A + B) dengan metoe jajar genjang:
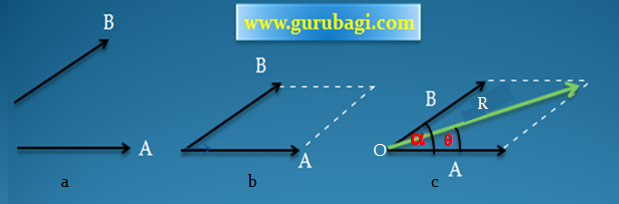
Keterangan :
a. Gambar vektor A dan B pada skala panjang yang sesuai.
b. Gambar vektor B dengan skala yang sesuai dimulai dari pangkal milik A, sehingga pangkal A bertemu dengan pangkal B, lalu buat garis proyeksi A dan garis proyeksi B hingga membentuk jajaran genjang.
c. Tarik garis resultan dari pangkal vektor ke sudut garis proyeksi ajar, dapat dilihat pada gambar di atas.
Sedangkan untuk besar panjang R dapat dirmuskan sebagai berikut :
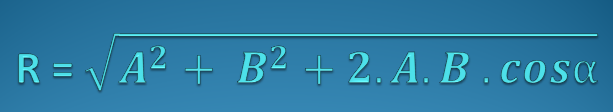
Keterangan :
R = Resultan vektor
A = Vektor pertama
B = Vektor kedua
α = Sudut apit kedua antara kedua vektor
Adapun untuk mencari arah R dapat dicari dengan menggunakan rumus persamanaan sinus sebagai berikut :
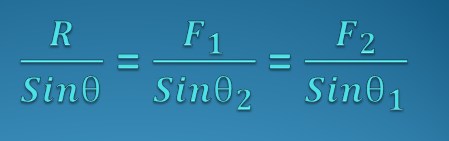
Baca : Resultan Vektor dengan Metode Segitiga dan Contoh Soalnya
Contoh Soal dan pembahasan
- Jika terdapat dua buah vektor P dan Q membentuk sudut ∝ sebesar 45 derajat seperti gambar di bawah ini.
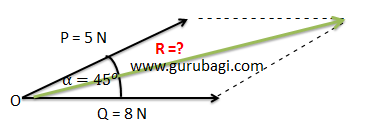
Tentukan resultan vektor pada gambar di atas!
Pembahasan :
Diketahui:
Vektor P = 5 N
Vektor Q = 8 N
α = 45o
Ditanyakan :
R ?
Jawab :
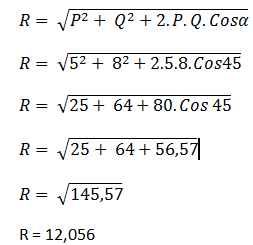
2. Diberikan dua buah vektor gaya yang sama besar masing-masing vektor besarnya adalah 10 Newton seperti gambar berikut.
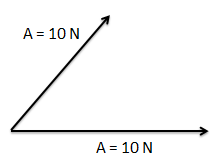
Jika sudut yang terbentuk antara kedua vektor adalah 60°, tentukan besar (nilai) resultan kedua vektor!
Pembahasan :
Gambar resultan untuk dua buah vektor yang telah diketahui sudutnya dapat dilihat dari metode jajar genjang berikut.
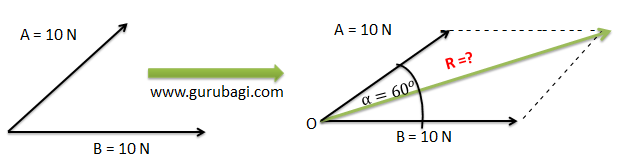
Diketahui:
Vektor A = 10 N
Vektro B = 10 N
Sudut α = 60o
Ditanyakan : R?
Jawab :
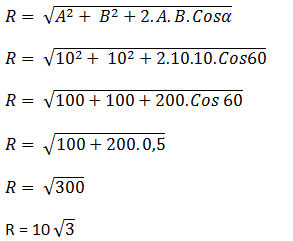
3. Diketahui dua buah vektor masing-masing panjangnya 6 cm dan 8 cm. Jika kedua vektor berimpit dan saling tegak lurus, maka tentukan arah resultan vektor tersebut terhadap kedua vektor dengan sudut 90o.
Pembahasan :
Diketahui :
Jika di buat keladam gambar akan terlihat seperti pada gambar di bawah ini :
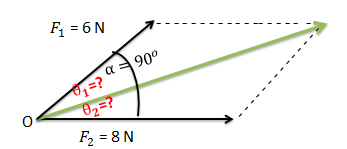
Dari gambar di atas dapat diketahui :
F1 =6 cm,
F2 = 8 cm
α = 900
Ditanyakan :
θ1 dan θ2
Jawab :
Untuk mencari θ1 dan θ2. terlebih dahulu mencari resultan vektor (R) dengan rumus dibawah ini.
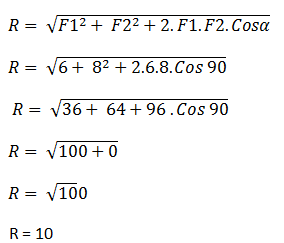
Setelah R ditemukan maka mencari θ1 terlebih dahulu dengan menggunakan rumus sinus.
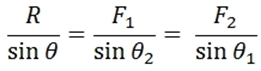
Persamaan sinus di atas sesuai yang kita gunakan menjadi seperti persamaan berikut ini:
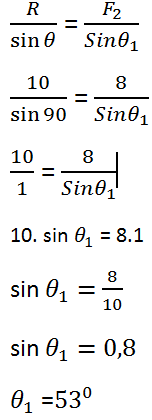
Selanjutnya mencari θ2, langsung menggunakan seisih sudut:
θ = θ1 + θ2
θ2 = θ – θ1
θ2 = 90o – 53o
θ2 = 37o
Maka di dapatkan θ1 = 53o dan θ2 = 37o
4. Jika diketahui dua buah vektor masing-masing panjangnya 10 N dan 5 N. Jika kedua vektor berimpit dan saling tegak lurus, maka tentukan besar dan resultan vektor, ika kedua vektor memiliki sudut 90o.
Pembahasan :
Diketahui :
F1 = 10 N
F2 = 5 N
α = 900
Ditanyakan :
a. Besar resultan vektor(R)?
b. Arah resultan vektor?
jawab :
a. Menentukan resultan vektor (R) dengan rumus berikut ini

b. Arah resultan vektor
Arah resultan vektor menggunakan persamaan di bawah ini.
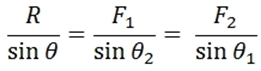
Arah resultan vektor dihitung terhadap F2, sehingga menggunakan persamaan berikut ini:
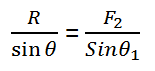
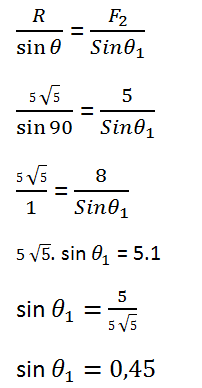
Demikian penjumlahan vektor metode jajar genjang berikut contoh soalnya. Semoga bermanfaat